Profit Server уже почти 10 лет работает в сфере предоставления услуг по аренде выделенных
Ищете хостинг или виртуальный сервер с комфортными условиями по оплате и использованию? Такие решения
Перечень операций в рамках настройки 1С и стоимость услуг зависит от специфики компании, внедряемого/настраиваемого
При заказе VPS/VDS от CloudVPS можно воспользоваться готовыми дистрибутивами для быстрого старта.
JUSTHOST — провайдер услуг, у которого есть все необходимое для уверенного присутствия в интернете.
Согласно статистике ежегодно российские маркетплейсы растут x2. Это касается, как заработка самих площадок, так
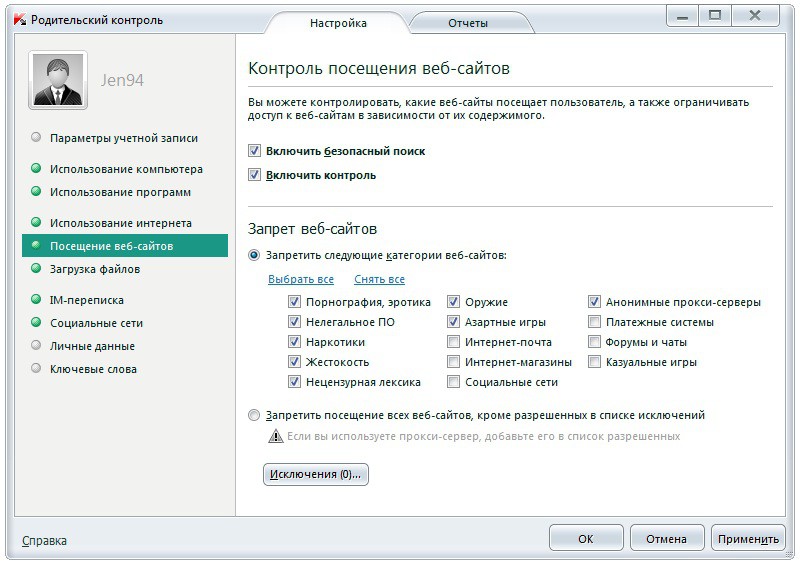
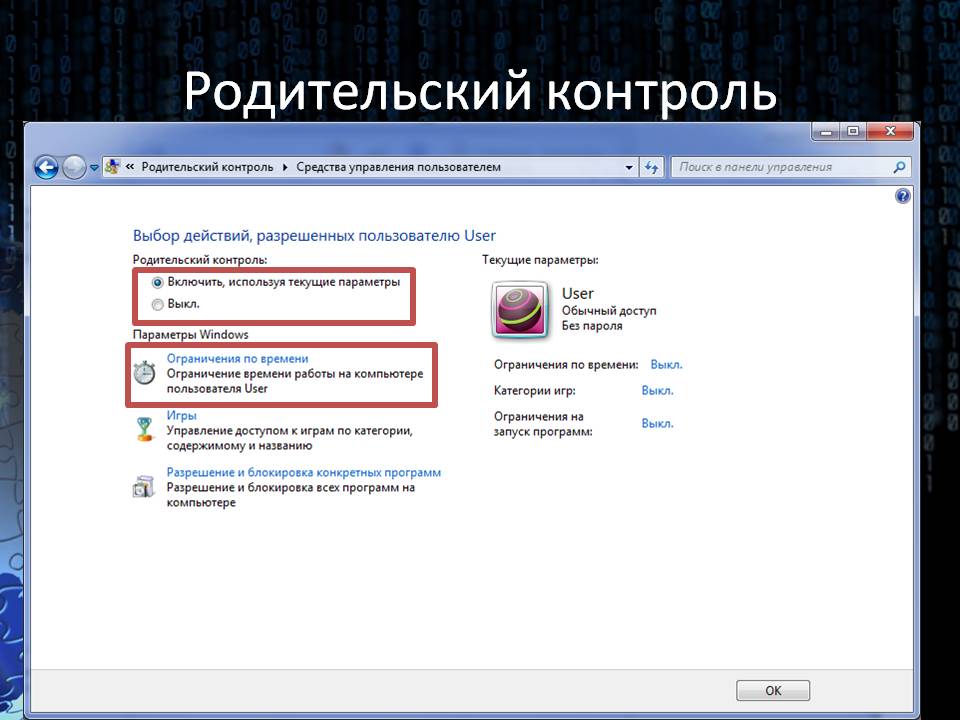
Мы разберем 10 лучших приложений по родительскому контролю 2021. А Вы уже сами решайте,
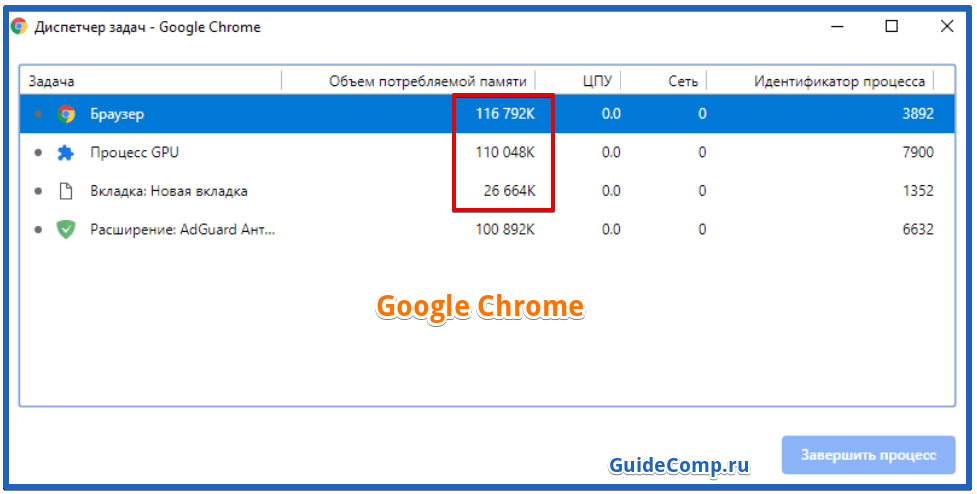
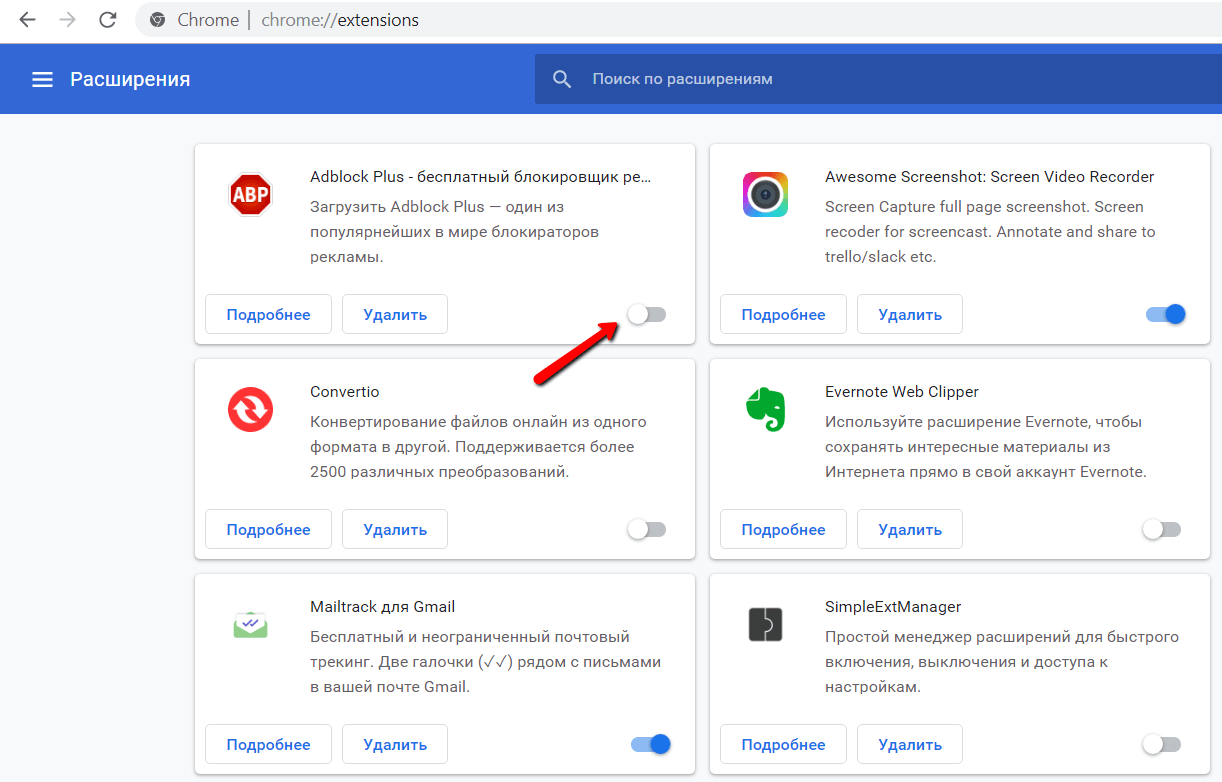
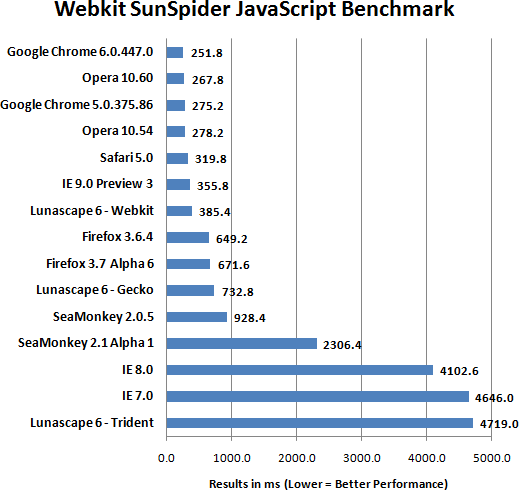
Разберёмся какие есть браузеры для Windows 7/8/10, популярные и не очень. Выясним какой браузер
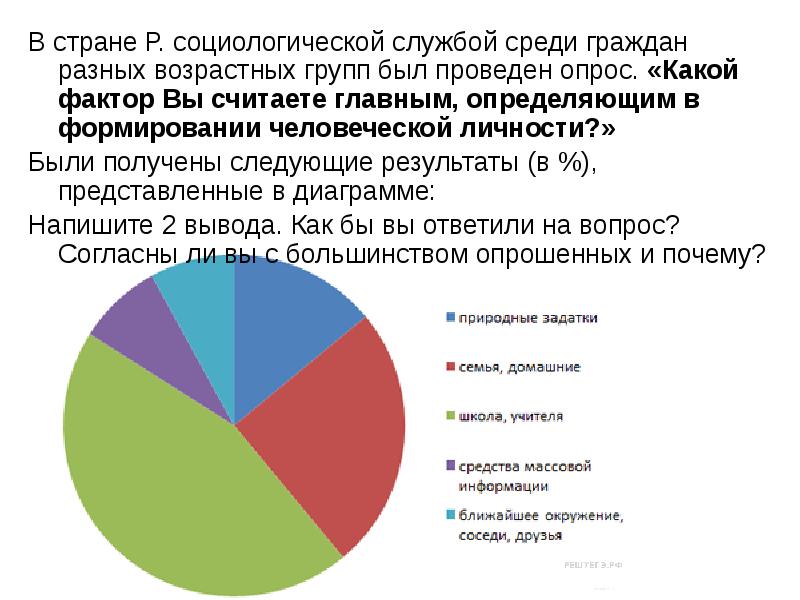
Социологическая служба страны z проводила опрос группы граждан Социологическая служба страны Z провела опрос
Любой, кто сделал покупку онлайн, имел кошмар о краже личных данных. Хотя эта проблема
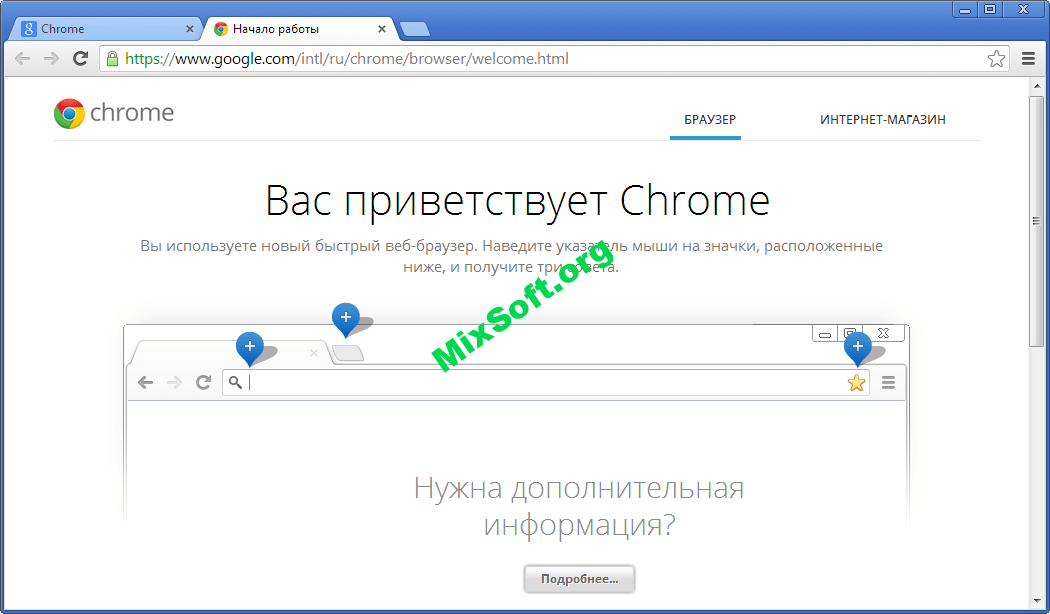
Сегодня мы поговорим о том, как появился браузер Google Chrome. История создания этого браузера
Беспроводная передача файлов довольно сильно эволюционировала за последние 15 лет. Олдфаги почти наверняка помнят,
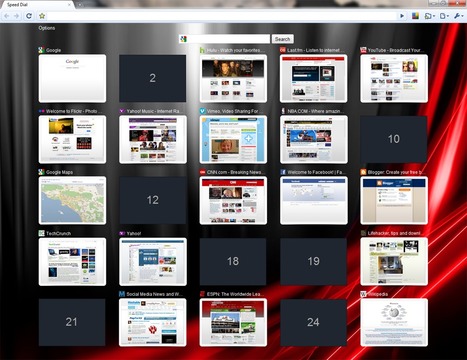
Speed Dial для Google Chrome – это весьма полезное расширение, которое облегчает работу с
Open Server Panel — это портативная серверная платформа и программная среда, созданная специально для
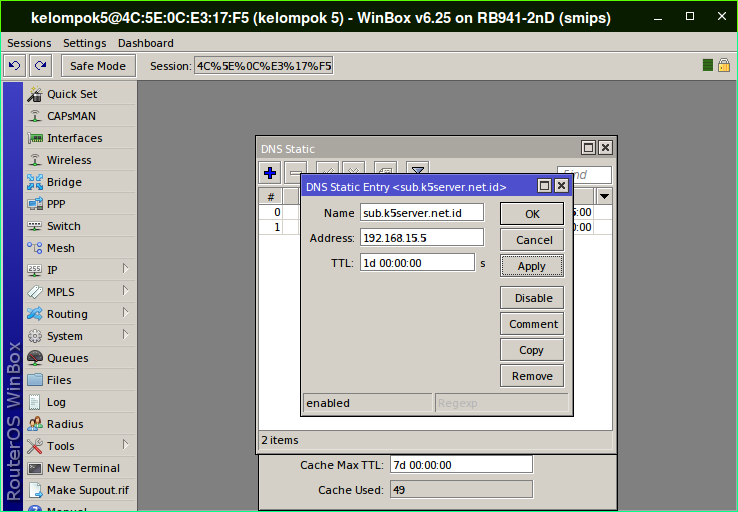
Администрирование компьютерных сетей – комплекс целенаправленных воздействий, проводимых для организации работы сети согласно определенной
Яндекс Браузер или Google Chrome-что лучше. Сравнение основных характеристик и ключевых параметров работы этих
Опасности теневого интернета могут угрожать даже тем, кто никогда не посещал эту часть Сети.
Краткая история эволюции мессенджеров — от отдельных настольных программ 80-х годов, до современных мобильных
Вопрос «Яндекс.Браузер или Google Chrome: что лучше» постоянно интересует тех, кто хочет узнать различия
Выполнение многих часто выполняемых операций может занимать длительное время. There are many commonly performed
«Главный антивирус — у вас в голове»: как работают шпионские компьютерные программы и существует
Интернет задумывался свободным. Прошло время, он обогнал по посещаемости традиционные СМИ и наткнулся на
Сегодня с чувством выполненного долга я наконец-то могу вздохнуть свободно. Как и обещал, выкладываю
Спорить, определяя лучший браузер для Windows, это тоже самое, что выяснять, какой цвет красивее,